Acwing数据结构
链表和邻接表
我们来创建链表的时候不会采用这种创建动态链表的方式,这种方式非常的慢,数据一旦多了会更慢,所以我们基本都用数组模拟链表,使用数组模拟链表最大的好处就是快、精准,之所以创建动态链表的方式更慢是因为在js中,new()这个操作是非常慢的
struck Node
{
int val;
Node *next;
}//不讲这种
new Node();//非常慢数组模拟单链表
做链表问题的时候最好是画一个图
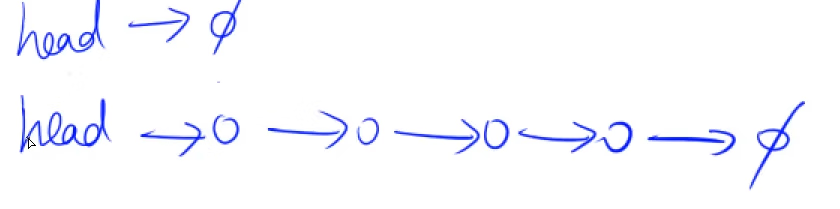
在单链表中,最常用的就是邻接表,邻接表最常用的用途是:
-
存储图
-
存储树
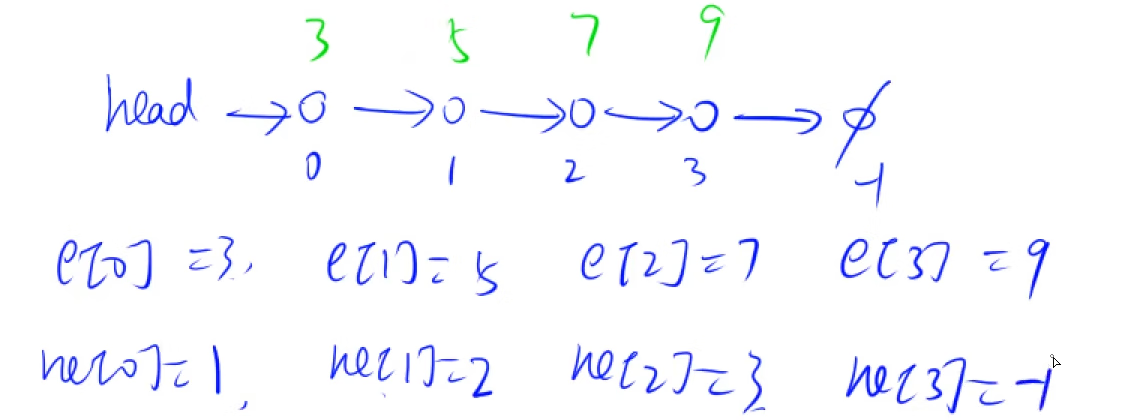
此处的
head表示头结点的下标,e[]为节点i的值,ne[]为next指针所指向的节点,在这里,空节点用-1来表示
单链表插入头结点
在头结点插入一个新节点的示意图(先拴新绳,再解旧绳)

idx存储当前已经用到了哪个点
代码示例:
void add_to_head(int x)
{
//先存储值
e[idx]=x;
//再让next指针指向新的节点
ne[idx]=head;
//最后让head再指向新加入的节点
head=idx;
//此时idx已经用过了,所以idx进入下一个节点
idx++;
}单链表的插入
将x节点插入到下标是K的节点的后面:(操作步骤与插入头结点差不多)
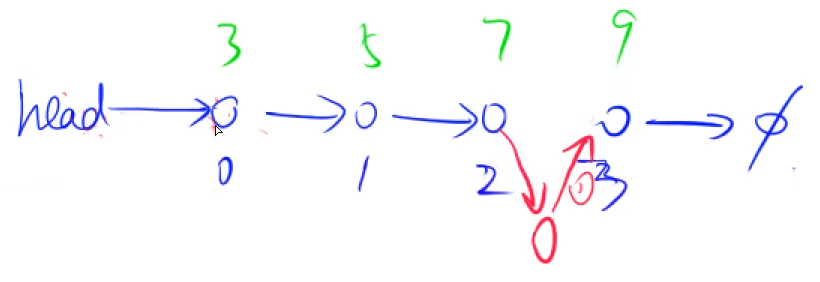
void add(int k,int x)
{
e[idx]=x;
ne[idx]=ne[k];
ne[k]=idx;
idx++;
}单链表的删除操作
将下标是k的点后面的点删除

void remove(int k)
{
//直接跳过中间的节点即可
ne[k]=ne[ne[k]];
}注意:单链表是单向不可逆的,如果我想删除在k之前的节点,是没有任何办法的,只能从头开始进行遍历
算法题里,不要去考虑内存泄露的问题,不然会钻牛角尖的
双链表
最常见的用处是优化某些问题
双链表与单链表不同的地方在于,双链表有两个指针,一个指向前,一个指向后
e[n]表示这个点的值,l[n]表示这个点左边的值,r[n]表示这个点右边的值,idx表示存储当前已经用到了哪个点
插入结点
在下标是k的点的右边插入一个点:
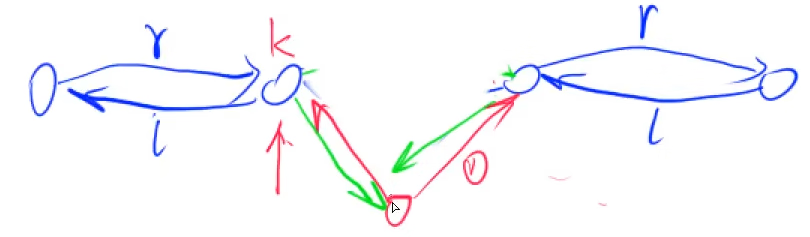
代码示例:
void add(int k,int x)
{
e[idx]=x;
r[idx]=r[k];
l[idx]=k;
l[r[k]]=idx;
r[k]=idx;
}在下标k的点的左边插入一个点:
add[l[k],x]//在k的左边这个点的右边插入x删除结点
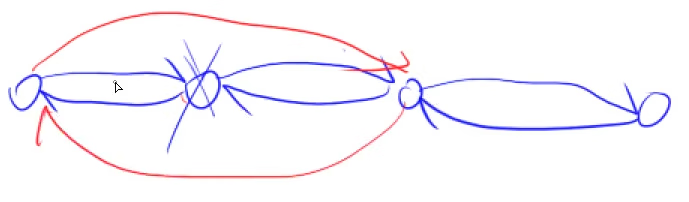
void remove(int k)
{
r[l[k]]=r[k];
l[r[k]]=l[k];
}栈
先进后出
每次只在其中的一端进行操作
// tt表示栈顶
int stk[N], tt = 0;
// 向栈顶插入一个数
stk[ ++ tt] = x;
// 从栈顶弹出一个数
tt -- ;
// 栈顶的值
stk[tt];
// 判断栈是否为空
if (tt > 0)
{
}队列
先进先出
队列分为普通队列和循环队列
普通队列:
// hh 表示队头,tt表示队尾
int q[N], hh = 0, tt = -1;
// 向队尾插入一个数
q[ ++ tt] = x;
// 从队头弹出一个数
hh ++ ;
// 队头的值
q[hh];
// 判断队列是否为空
if (hh <= tt)
{
}循环队列:
// hh 表示队头,tt表示队尾的后一个位置
int q[N], hh = 0, tt = 0;
// 向队尾插入一个数
q[tt ++ ] = x;
if (tt == N) tt = 0;
// 从队头弹出一个数
hh ++ ;
if (hh == N) hh = 0;
// 队头的值
q[hh];
// 判断队列是否为空
if (hh != tt)
{
}单调栈
最常见的题型:返回左边离它最近的比它小的数,若没有,则返回负一

常见模型:找出每个数左边离它最近的比它大/小的数
int tt = 0;
for (int i = 1; i <= n; i ++ )
{
while (tt && check(stk[tt], i)) tt -- ;
stk[ ++ tt] = i;
}单调队列

最经典的应用就是求滑动窗口的最小值/最大值
常见模型:找出滑动窗口中的最大值/最小值
int hh = 0, tt = -1;
for (int i = 0; i < n; i ++ )
{
while (hh <= tt && check_out(q[hh])) hh ++ ; // 判断队头是否滑出窗口
while (hh <= tt && check(q[tt], i)) tt -- ;
q[ ++ tt] = i;
}
通过单调队列来维护窗口,当窗口向右移动的时候,需要先插入新的数,然后删除最左边的数,以此来维护窗口(最开始没有达到窗口数量限制时,只需进队)
KMP
KMP我们先来尝试一下暴力做法:
暴力做法进行匹配 当前面的都与另一个字符串(较长的)相同时,继续匹配;当遇见不一样的时候,将整个字符串(较短的那个),往后移动一位,再进行匹配,直到能够再进行匹配为止

for (int i = 1; i <= n; i ++ )
{
bool flag = true;
for (int j = 1; j <= m; j ++ )
{
if (s[i + j - 1] ! = p[j])
{
flag=false;
break;
}
}
}优化思路:由于有重合的字符串片段,所以我们应该对每一个点进行预处理,从1->j这一段和从i-j+1->i这一段是相等的
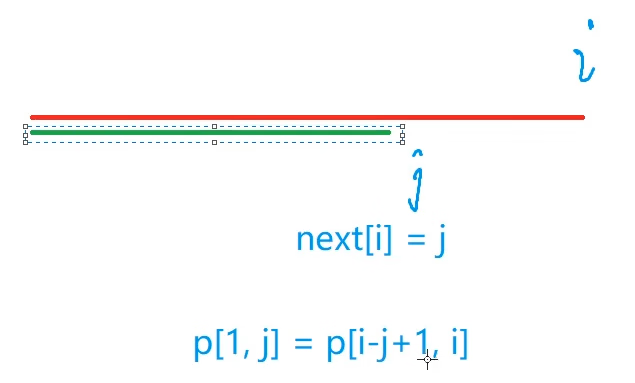
匹配过程: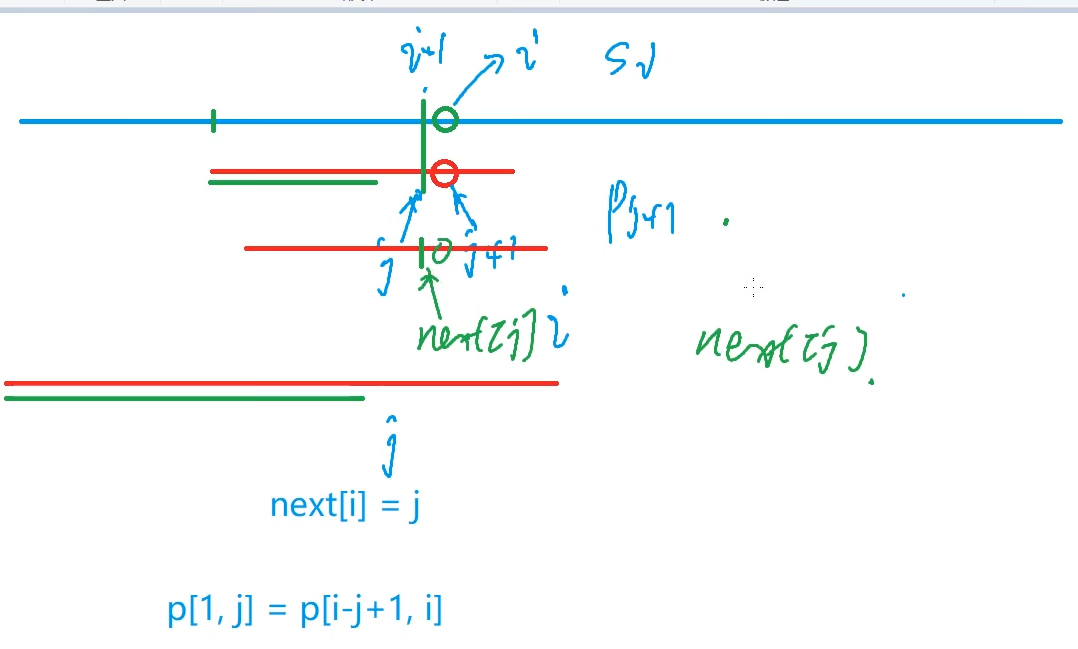
// s[]是长文本,p[]是模式串,n是s的长度,m是p的长度
求模式串的Next数组:
for (int i = 2, j = 0; i <= m; i ++ )
{
while (j && p[i] != p[j + 1]) j = ne[j];
if (p[i] == p[j + 1]) j ++ ;
ne[i] = j;
}
// 匹配
for (int i = 1, j = 0; i <= n; i ++ )
{
while (j && s[i] != p[j + 1]) j = ne[j];
if (s[i] == p[j + 1]) j ++ ;
if (j == m)
{
j = ne[j];
// 匹配成功后的逻辑
}
}例子:

Trie树(单词查找树/字典树)
哈希树的一个变种,用来快速存储和查找字符串集合的数据结构,存储的字母类型不会很多(一般要么全是小写字母 要么全是大写字母 要么全是0 1)
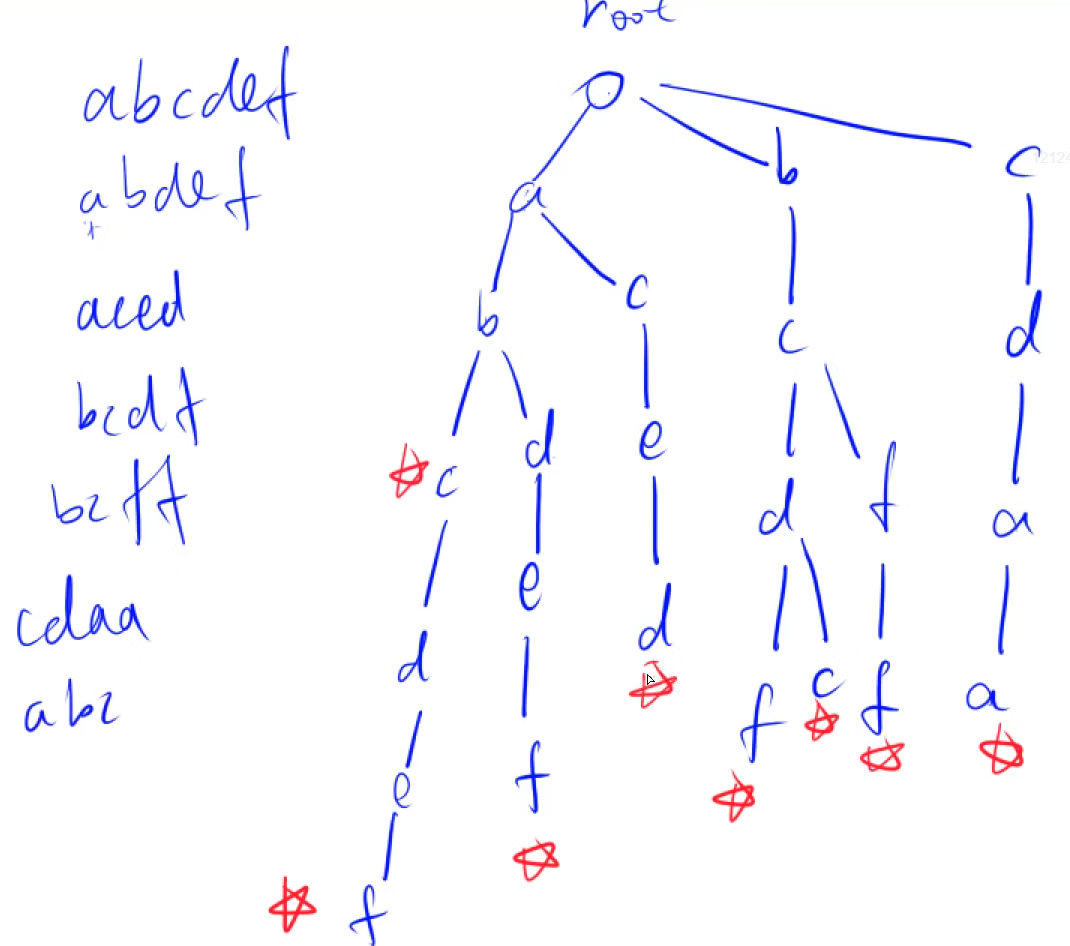
将字母存储在里面,每次都从根节点开始存储,如果前面有相同的路径,就不需要再重复写一个路线,继续沿着之前相同的路线走,直到出现不同的字母才产生新的分支(例如这里的abcdef和abdef,ab是两个共有的,就无需重写,直接在b处再分开即可) 单词的结尾处会加上一个标记,便于后续的查找
int son[N][26], cnt[N], idx;//用数组来模拟指针
// 0号点既是根节点,又是空节点
// son[][]存储树中每个节点的子节点
// cnt[]存储以每个节点结尾的单词数量
// 插入一个字符串
void insert(char *str)
{
int p = 0;
for (int i = 0; str[i]; i ++ )
{
int u = str[i] - 'a';//为了将小写字母a——z给映射成0——25,所以将其减去a
if (!son[p][u]) son[p][u] = ++ idx;//如果不存在这个子节点的话,就自己创建一个
p = son[p][u];//走过去
}
cnt[p] ++ ;
}
// 查询字符串出现的次数
int query(char *str)
{
int p = 0;
for (int i = 0; str[i]; i ++ )
{
int u = str[i] - 'a';
if (!son[p][u]) return 0;//如果不存在这个子节点的话,返回0即可
p = son[p][u];
}
return cnt[p];
}并查集
竞赛和面试的时候很容易考察的,因为其代码短,思路精巧、
并查集的操作:
- 将两个集合合并
- 询问两个元素是否在一个集合当中
基本原理:每一个集合我们用一个
树来表示,树根的编号就是整个集合的编号。每个节点存储它的父节点,p[x]表示x的父节点
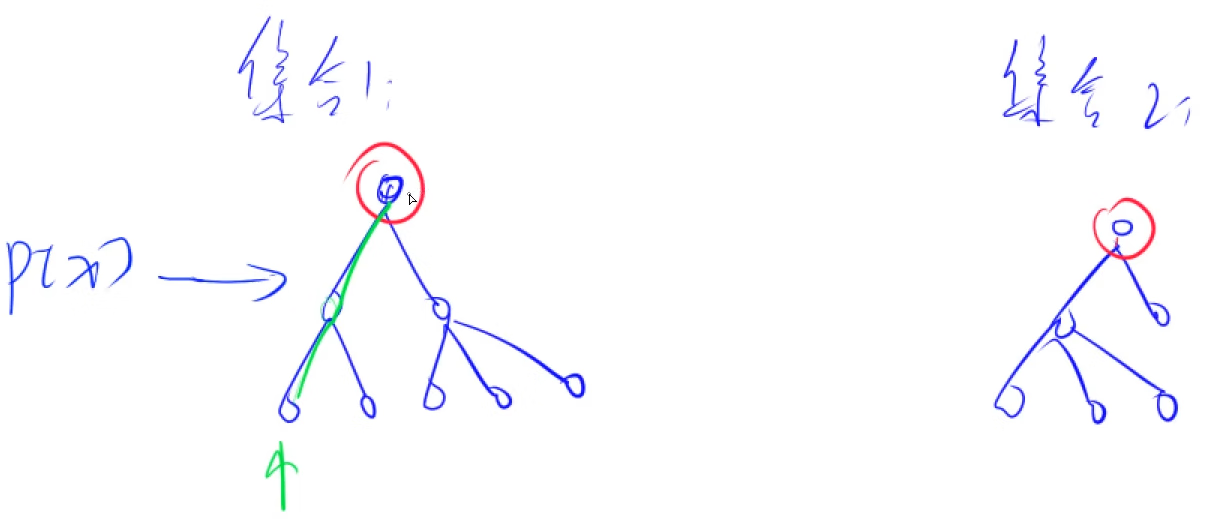

优化方式:路径压缩:当我们找到根节点后,将这条路径上的所有节点全部指向根节点,之后再进行查询的话就直接可以指向root了,时间复杂度几乎达到了O(1)
(1)朴素并查集:
int p[N]; //存储每个点的祖宗节点
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ ) p[i] = i;
// 合并a和b所在的两个集合:
p[find(a)] = find(b);
(2)维护size的并查集:
int p[N], size[N];
//p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义,表示祖宗节点所在集合中的点的数量
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ )
{
p[i] = i;
size[i] = 1;
}
// 合并a和b所在的两个集合:
size[find(b)] += size[find(a)];
p[find(a)] = find(b);
(3)维护到祖宗节点距离的并查集:
int p[N], d[N];
//p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x)
{
int u = find(p[x]);
d[x] += d[p[x]];
p[x] = u;
}
return p[x];
}
// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ )
{
p[i] = i;
d[i] = 0;
}
// 合并a和b所在的两个集合:
p[find(a)] = find(b);
d[find(a)] = distance; // 根据具体问题,初始化find(a)的偏移量